geometry .com

What is Parallelogram?

A parallelogram is a special type of quadrilateral that has equal and parallel opposite sides. 

The given figure shows a parallelogram ABCD which as AB parallel to CD and AD parallel to BC.

Also, AD = BC and AB = CD.

 

We also see a lot of parallelogram like shapes and objects around us. 

 

Properties of parallelogram

 

	The opposite sides of a parallelogram are parallel to each other.  Here, AB ∥ CD and AD ∥ BC
	The opposite sides of a parallelogram are equal in length.  Here, AB = CD and AD = BC
	The opposite angles of a parallelogram are equal in measure.  Here, Angle A = Angle C and  Angle B = Angle D.
	Adjacent angles of a parallelogram add up to 180°  Here, Angle A + Angle B = 180°  Angle B + Angle C = 180°  Angle C + Angle D = 180°  Angle D + Angle A = 180°
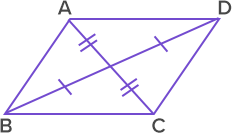	Diagonals of a parallelogram bisect each other.  Here AC and BD bisect each other.

 

Types of a parallelogram

There are three special types of a parallelogram.

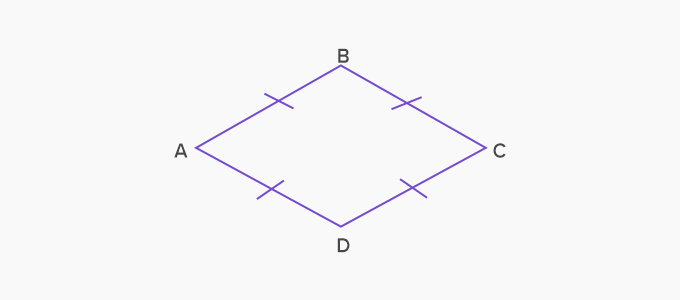
 1. Rhombus: A parallelogram in which all sides are equal.

Here AB = BC = CD = DA.  ABCD is a rhombus.

 

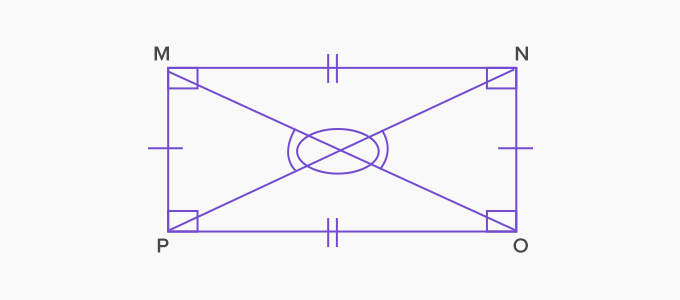
 2. Rectangle: A parallelogram in which all angles are right angles and the diagonals are equal.

 

Here all angles are right angles. Diagonals PN and OM are equal.

 

 3. Square: A parallelogram with all equal sides and all angles equal to 90 degrees. The diagonals of a square are also equal.

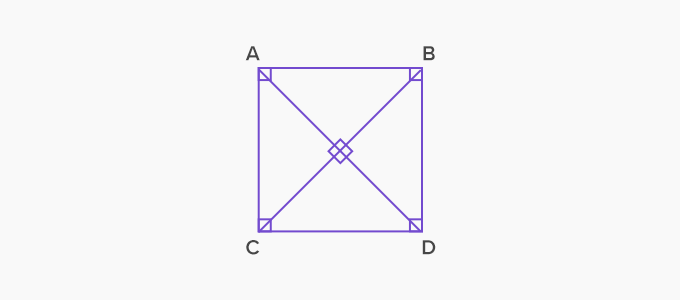
Here all sides are equal and all the angles are right angles.

Diagonals AC and BD are equal.

What is tringle-:

a plane figure with three straight sides and three angles.

A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted ${\displaystyle \triangle ABC}$.^[1]

Equilateral triangle

A regular triangle. A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Circle A circle (black), which is measured by its circumference (C), diameter (D) in blue, and radius (R) in red; its centre (O) is in green. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a disc. A circle may also be defined as a special kind of ellipse in which the two foci are coincident and the eccentricity is 0, or the two-dimensional shape enclosing the most area per unit perimeter squared, using calculus of variations.